Bias Variance: The impact and relevance in Artificial Intelligence & Machine Learning.

Bias variance tradeoff is one of those terms that a lot of people talk about in data science but few have a proper nuanced understanding of the concept. Let's change that today with this discussion. Before we hit it off with a bias-variance discussion, let's remind ourselves about what we are trying to achieve when we build a predictive model for any problem.

Three things to keep in mind for Bias and Variance in Machine Learning:

• We are trying to extract consistent patterns from the historical data which we expect will persist in future.[after all, our goal is to make predictions for future data with this model]
• Historical data is going to have noisy patterns which will not persist in the future
• Our basic assumption is that any pattern which is backed by a good amount of data is going to persist, and which is not backed by a good amount of data is not going to persist and should be ignored by some mechanism

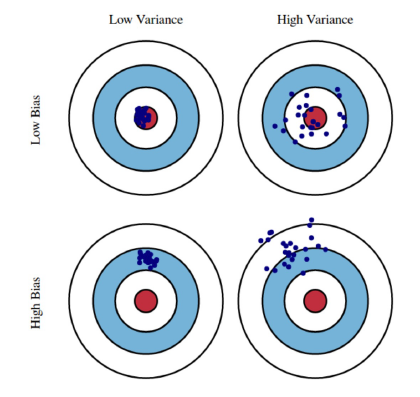
Imagine the centre of the red bulls' eye region is the true mean value of our target random variable which we are trying to predict. Every time we take a sample set of observations and predict the value of this variable we plot a blue dot. We predicted correctly if the blue dot falls inside the red region. Bias is the measure of how far off the predicted blue dots are from the centre of the red region (the true mean). Intuitively bias is a quantification of error. Variance is how scattered are our predictions.

The top left is the ideal condition but it is hard to achieve in practice, and the bottom right is the worst-case scenario which is easy to achieve in practice (usually the starting condition for randomly initialised models). Our goal is to go from the bottom right (high bias high variance) situation to the top left situation (low variance low bias).

But the problem here is: Unfortunately, achieving the lowest variance and lowest bias simultaneously is hard. When we try to decrease one of these parameters (either bias or variance), the other parameter increases.

Now the trade-off here is:

There is a sweet spot somewhere in between which produces the least prediction error in the long run.

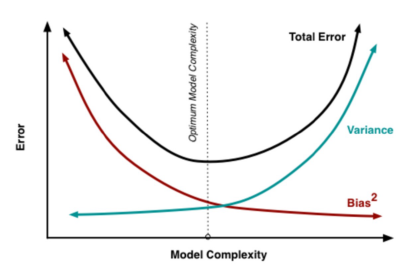
You need to understand that bias-variance tradeoff discussion is done at the algorithm level. It is not specific to any single problem or model.

Let me summarise and reiterate a few of the things that we discussed :

• Error due to Bias: The error due to bias is taken as the difference between the expected (or average) prediction of our model and the correct value that we are trying to predict. Of course, you only have one model so talking about expected or average prediction values might seem a little strange. However, imagine you could repeat the whole model building process more than once: each time you gather new data and run a new analysis creating a new model. Due to randomness in the underlying data sets, the resulting models will have a range of predictions. Bias measures how far off in general these models' predictions are from the correct value.
• Error due to Variance: The error due to variance is taken as the variability of a model prediction for a given data point. Again, imagine you can repeat the entire model building process multiple times. The variance is how much the predictions for a given point vary between different realisations of the model.

So simpler models make use of very generic patterns and cannot capture very nuanced patterns present in the data. The basic logic here is -

• Generic patterns in the data do not sample-specific, meaning from one data sample to another, generic patterns do not change dramatically
• Nuanced patterns however can be at times noisy or very sample-specific. High chances that the pattern that you see in a small subset of the data does not generalise or persist in the future.

So simpler models are consistent across different data samples, their variance will be low, predictions will be consistent, and they will generalise relatively better. However, this comes at the cost of, predictions not being very accurate: meaning high bias.

More complex models will be capturing nuanced patterns and hence their predictions will tend to be more accurate, hence low bias. However, they will not be relatively consistent with a change in data samples, leading to high variance.

Parting thoughts

IBM’s reformative vision towards education in Artificial Intelligence and Machine Learning makes it a showstopper in the jungle of byte-sized and macro-level learning paths that is co-developed with thoughts leaders of the industry to ensure that your career takes off with the invincible competency under the right mentorship under IBM academicians.